Pharmacy calculation/dilutions calculators

Abbreviations and symbols: Medical abbreviations and symbols are a shorthand language used in the healthcare field to communicate essential information efficiently. As a student, it is important to familiarize yourself with these abbreviations and symbols to effectively understand medical documentation, prescriptions, and patient charts. By learning and utilizing these standardized abbreviations and symbols, you will be able to communicate and interpret medical information accurately, ensuring safer and more effective patient care.

Practical problems

Q1: What is the final concentration of drug X if 25 mL of 10 mg/mL of the solution is mixed with 10 mL of a 4 mg/mL solution?

Equation: C1xV1+C2xV2=CfxVF

Given:

C1: 10 mg/mL

V1: 25 mL

C2: 4 mg/mL

V2: 10 mL

Calculation:

Vf=V1+V2=25 + 10 =35 mL

Cf=(C1xV1+C2xV2)/Vf=(10 x 25+ 4x10)/35=8.29 mg/mL

Q2: A pharmacist poured a 20 mL of 4% NaCl solution into a flask, which already containing 8% of NaCl 25 mL, what is the final NaCl concentration?

Equation: C1xV1+C2xV2=CfxVF

Given:

C1: 4%

V1: 20 mL

C2: 8%

V2: 25 mL

Calculation:

Vf=V1+V2=20 + 25 =45 mL

Cf=(C1xV1+C2xV2)/Vf=(4% x 20+ 8%x25)/45=6.22%

Q3: When you mix a 10 % NaCl solution 10 mL with another 400 mL NaCl solution, the final concentration is 0.9%, what is the concentration of the second solution?

Equation: C1xV1+C2xV2=CfxVF

Given:

C1: 9%

V1: 10 mL

C2: unknown

V2: 400 mL

Cf: 0.9%

Vf=10+400=410 mL

Calculation:

C2=((CfxVf-C1xV1)/V2

C2=(0.9 %x410-10% x 10 mL)/400=0.6725%

Significant figure: Digits that have practical consequences in pharmacy 

  1. Zero is significant. What is the difference between 19.120 mL (5 significant figures) and 19.12 mL (4 significant figures)?  
  2. Zero indicates the location of decimal point. What is the difference between 0.192 mL (3 significant figures) and 0.0192 mL(3 significant figures) ?  
  3. The results of addition and subtraction: contain the same number of decimal places as the component with the fewest decimal places. All figures should be retained until the end, when rounding off is performed

      12.5 + 10.65 + 8.30 = 31.45 g =31.5 g       

 4. The results of products ad quotients should have no more significant figure than the component           with the smallest number of significant figure.

     2.466 mol/mL x 15 mL = 36.990 =37 mL     

Dimensional analysis: Analysis using numerical value and units (to avoid errors)

    1. A pharmacist wants to know how many inhalers should be dispensed to provide a 60 day supply of drug x. The recommended dose is 168 μg twice daily. The commercial inhaler delivers 42 μg per metered dose and contains 200 metered doses.

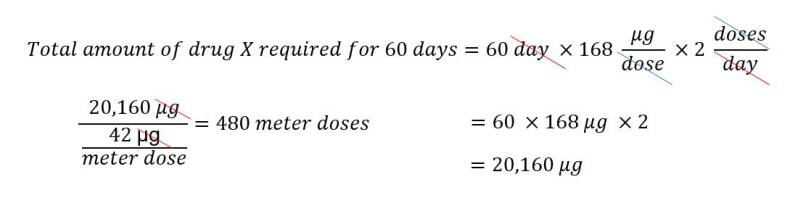
    2. Irinotecan is administered through i.v. infusion at 180 mg/m2 in one cycle. For a patient with 70.0 kg, how many mg of irinotecan is required for 6 cycles. (1 kg: 0.03 m2)

    Preventing errors
    • Handwriting must be legible for any person to read
    • A pharmacist should never guess at the meaning of an unclear work or an abbreviation that may be a shorthand creation of the individual prescriber
    • Avoid the use of certain traditional abbreviations
    • Always using the metric system
    • Clear drug information. Name, metric weight or concentration, type of dosage form.
    • A leading zero before the decimal point. (.5 mg x , 0.5 mg)
    • Have properly placed commas (e.g., 4123 mL x, 4,123 mL)
    • Prescribers shall provide the weight of the patient when possible (dose check).
    • Provide a notation of purpose of the medication when possible
    • Should not use imprecise instructions (e.g., take as needed)
    • Writing or computer prescription is preferred
    • If a prescription has omitted the desired drug strength or its dosage form, pharmacist should never dispense the prescription but consult the prescriber
    • To avoid error in liquid dosing, a calibrated measuring device should be dispensed with the liquid medication.
    • Five rights principle: 1), the right medication; 2) the right dose; 3) the right patient; 4) the right time, and 5) the right route of administration.

    Disclaimer: The web calculator provided on this platform is designed to assist students with calculations commonly encountered in their coursework. While every effort has been made to ensure the accuracy and reliability of the calculator, we cannot guarantee that it is error-free or that the results obtained will always be precise.

    It is important to note that this calculator should be used as a supplementary tool and not as a substitute for understanding the underlying concepts and principles of pharmaceutical calculations. It is always recommended to consult course materials, textbooks, and, if necessary, seek guidance from your instructors. In the event of any discrepancy or doubt, it is the responsibility of the user to seek clarification and confirm the correctness of the calculations through reliable sources.

    The creators of PharmCalculator cannot be held liable for any errors, inaccuracies, or consequences arising from the use of this tool. Students are encouraged to report any identified issues or feedback to continuously improve the calculator for future users.

    By using this calculator, you acknowledge that you have read and understood this disclaimer, and you agree to use the calculator at your own risk, taking full responsibility for any decisions or actions based on the results obtained.